Metode elemen hingga (Finite Element Method) yaitu menyusun sebuah obyek (sistem) yang kompleks dari beberapa elemen kecil yang sederhana dan atau membagi sebuah obyek (sistem) yang komplek menjadi beberapa bagian kecil yang dapat diatur (Liu, 2003). Analisis metode elemen hingga mendiskretisasi sebuah kontinum menjadi beberapa elemen dan di setiap elemen dipilih fungsi sederhana untuk memperkirakan variasi dan variabel lapangan seperti perpindahan dan tekanan pori (Agrensa, 2012).
Metode
elemen hingga digunakan untuk analisis tegangan dan deformasi. Geometri
material yang akan dianalisis terlebih dahulu dibagi menjadi jaring-jaring
elemen hingga, sehingga analisis akan menjadi lebih mudah. Metode elemen hingga
dapat digunakan untuk analisis material padat, termasuk analisis geoteknik pada
material tanah. Gambar 2.5 menunjukkan posisi tegangan pada material padat.
Metode
elemen hingga dapat digunakan untuk mengetahui modulus elastisitas suatu
material, parameter ini didefinisikan sebagai matrik hubungan tegangan-regangan
yang terjadi pada material akibat beban yang bekerja padanya. Matrik modulus
elastisitas terdiri dari komponen tegangan normal (σ) dan tegangan geser (τ),
serta regangan normal (ε) dan regangan geser (γ) pada arah sumbu x, y, dan z
dalam bidang kartesius seperti ditunjukan oleh persamaan (2.9) hingga (2.10)
Matrik
tegangan:
Matrik regangan:
Matrik Hubungan
Tegangan-regangan:
Salah
satu hal yang sangat penting dalam permodelan menggunakan elemen hingga adalah
menetukan model material. Model material adalah sekumpulan persamaan matematika
yang menjelaskan hubungan antara regangan-tegangan. Suatu material harus
dimodelkan secara mekanis menggunakan persamaan konstitutif. Penentuan model suatu
material dibuat sesuai material yang ditinjau serta derajat keakuratan yang
diinginkan.
Beberapa
model material yang digunakan dalam material tanah dan batuan misalnya Nonlinier Elasticity (Hiperbolic), Mohr-Coulumb
atau Elastic Plastic (MC) dan Hardening-Soil
(HS).
Masing-masing
model diatas memiliki parameter tersendiri serta memiliki kelebihan dan
kekurangan. Keakuratan permodelan menggunakan metode elemen hingga sangat
tergantung pada keahlian memodelkan, pemahaman terhadap model dan keterbatasannya,
pemilihan parameter dan model material tanah serta kemampuan menilai hasil
komputasi.
Penelitian
ini menggunakan model material tanah yaitu model tanah Mohr-Coulumb atau
Elastic Plastic (MC), model ini merupakan model material tanah yang paling
banyak dikenal karena perhitungannya yang relatif sederhana namun hasil yang
didapatkan cukup akurat, model ini juga mempunyai kelebihan untuk memodelkan
tanah pada kondisi elastis hingga plastis, dimana bentuknya seperti terlihat
pada Gambar 2.6 berikut:
Gambar
2.6 Model material mohr-coulumb (Brinkgreve et al., 2006)
Formulasi
model Mohr-Coulumb sekarang adalah perkembangan dari formulasi umum tegangan.
Hukum umum tegangan pada kenyatannya dipakai dalam seluruh elemen material.
Smith dan Griffith (1982) memformulasikan lengkap dari Mohr-Coulomb yang
memiliki enam fungsi yang merupakan hasil formulasi umum tegangan (Pramugani
dan Setiawan, 2007). Gambar tegangan model material Mohr-Coulomb dapat dilihat
pada Gambar 2.7.
Gambar
2.7 Tiga dimensi permukaan model mohr-coulumb
(Brinkgreve
et al., 2006)
Model
dengan sudut geser (ϕ) dan kohesi (c), mempresentasikan bentuk heksagonal
dalam menggambarkan tegangan utama. Model Mohr-Coulumb memiliki 6 fungsi
potensial, yaitu:
Model
Mohr-Coulumb akan stabil pada saat c > 0, sedangkan pada kenyataanya
tegangan naik seiring dengan naiknya kohesi oleh karena itu tension cut-off (kegagalan tanah akibat
kompresi) memperkenalkan fungsi tiga dimensi, yaitu:
Model
Mohr Coulumb membutuhkan lima parameter yang secara umum dapat didapatkan dari
tes tanah sederhana, yaitu modulus young
(E), kohesi (c), rasio poisson (v), sudut geser (ϕ), sudut dilatansi (ψ)
Progam Plaxis
terdiri dari 3 sub progam pada user
interface yaitu input, output dan curves. Input digunakan untuk mengatur geometri, parameter model dan fase
perhitungan. Output digunakan untuk
menampilkan hasil perhitungan. Curves
digunakan untuk melakukan plot grafik angka hasil.
Input
progam terdiri dari dua mode yang berbeda yairu Model dan Calculation. ModeModel berfungsi untuk membuat dan
mengatur model geometri dan untuk membuat jaring-jaring elemen hingga secara
dua dimensi dan tiga dimensi. ModeCalculation
berisikan semua fasilitas untuk mengatur fase perhitungan yang
merepresentasikan tahap-tahap yang berbeda dari pembebanan dan konstruksi
termasuk kondisi awal geometri.
Calculation
adalah mode yang digunakan untuk melakukan perhitungan pada Progam Plaxis. Perhitungan elemen hingga
dapat dibagi menjadi beberapa rangkaian fase perhitungan. Fase perhitungan
paling awal (InitialPhase) memperhitungkan
kondisi awal suatu model berdasarkan gravitasi (GravityLoading) atau prosedur k0 (k0Procedure). Setelah perhitungan awal ini, selanjutnya
perhitungan dapan dilakukan sesuai yang diinginkan.
Output
progam berisikan semua fasilitas untuk melihat hasil dari data yang dimasukkan
dan perhitungan elemen hingga secara tiga dimensi. Curves progam adalah suatu subprogram dari plaxis untuk menampilkan
kurva beban-perpindahan, garis tegangan dan diagram-diagram tegangan. Subprogam
ini hanya dapat diakses apabila titik-titik tinjauan telah ditentukan dahulu
sebelum perhitungan. Gambar model pondasi pada ProgamPlaxis3DFoundation dapat dilihat pada Gambar 2.8 sebagai
berikut.



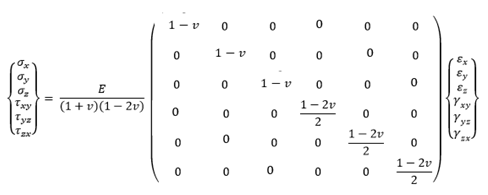






0 Komentar